Interface Conductance Modal Analysis (ICMA)
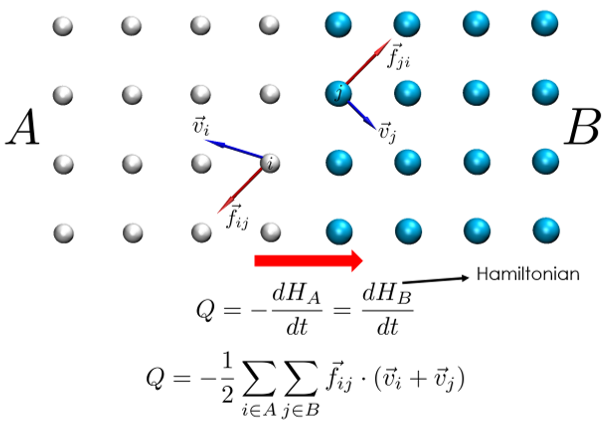
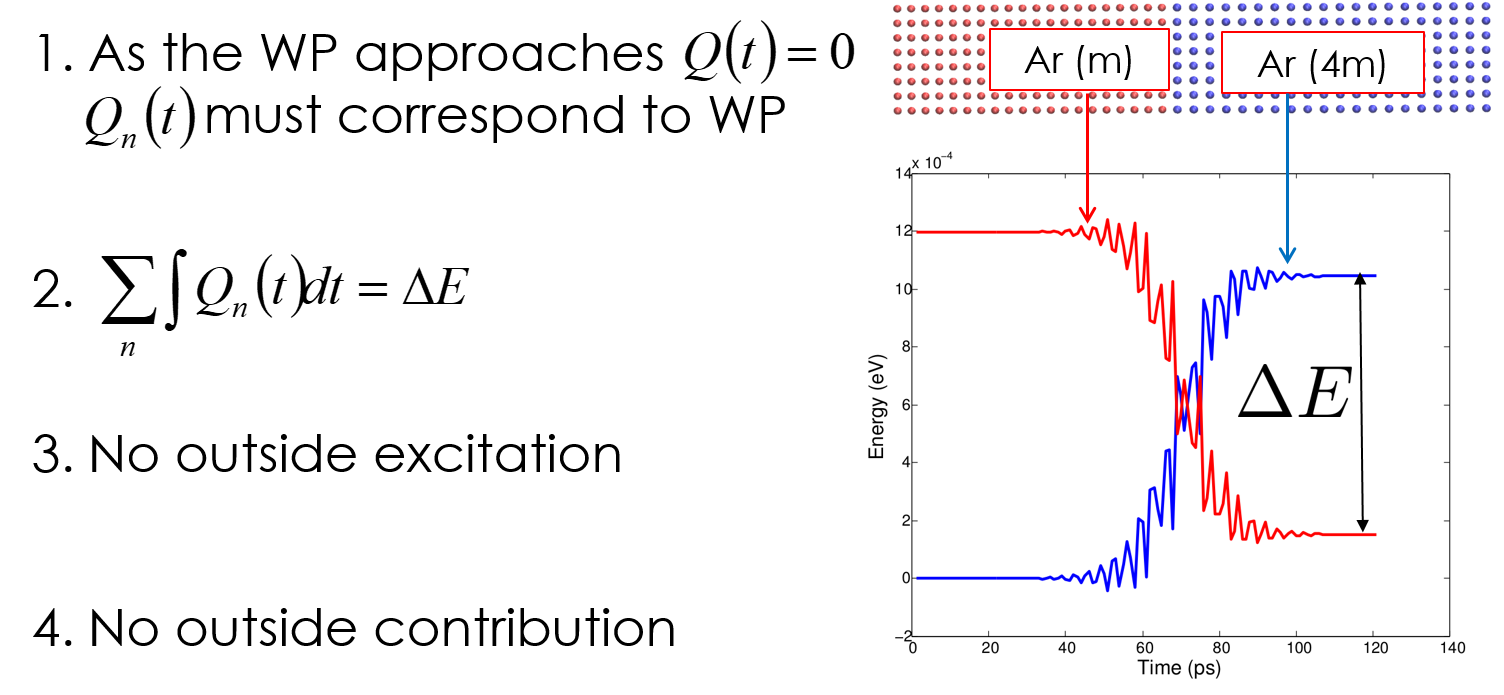
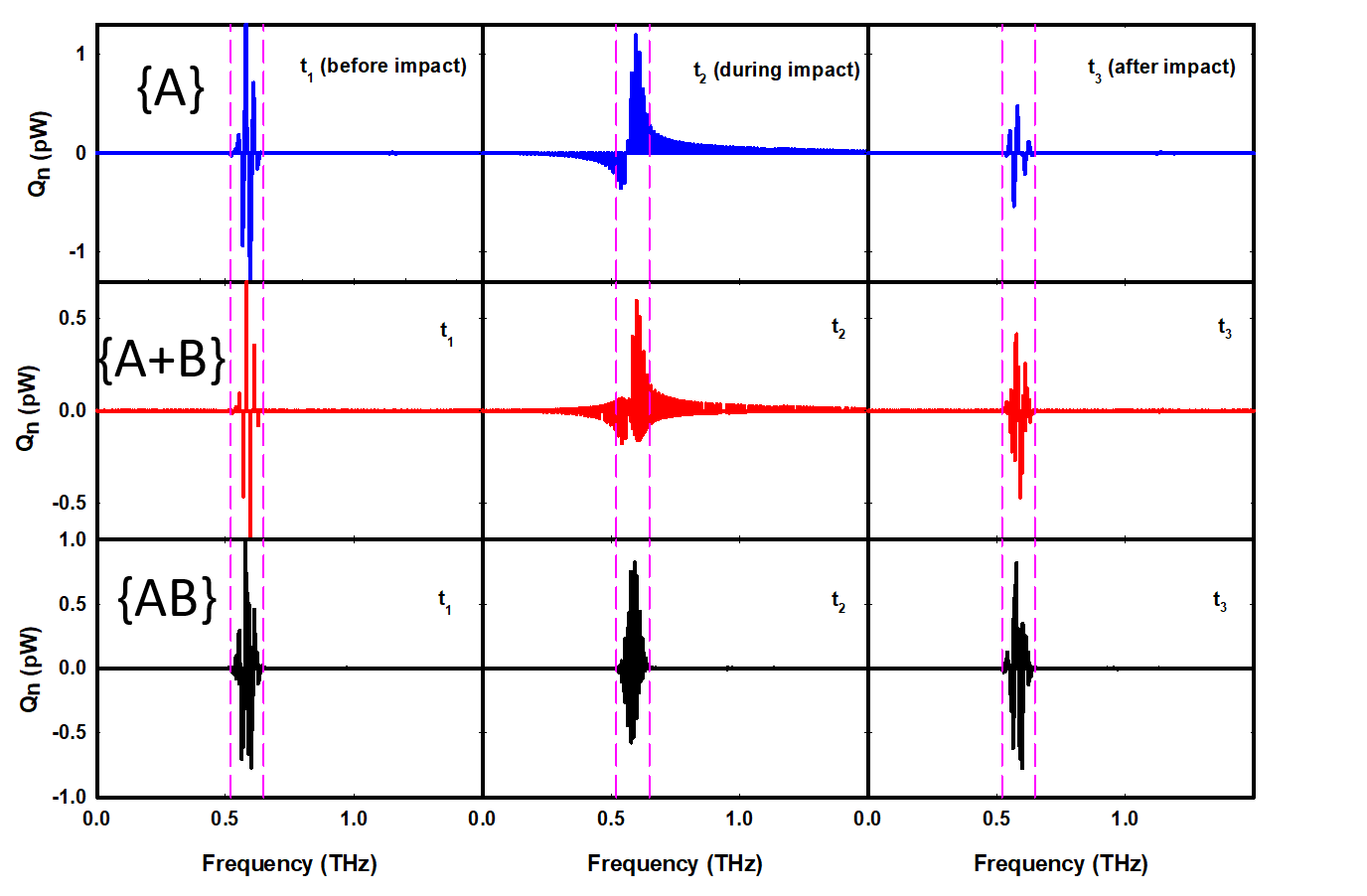
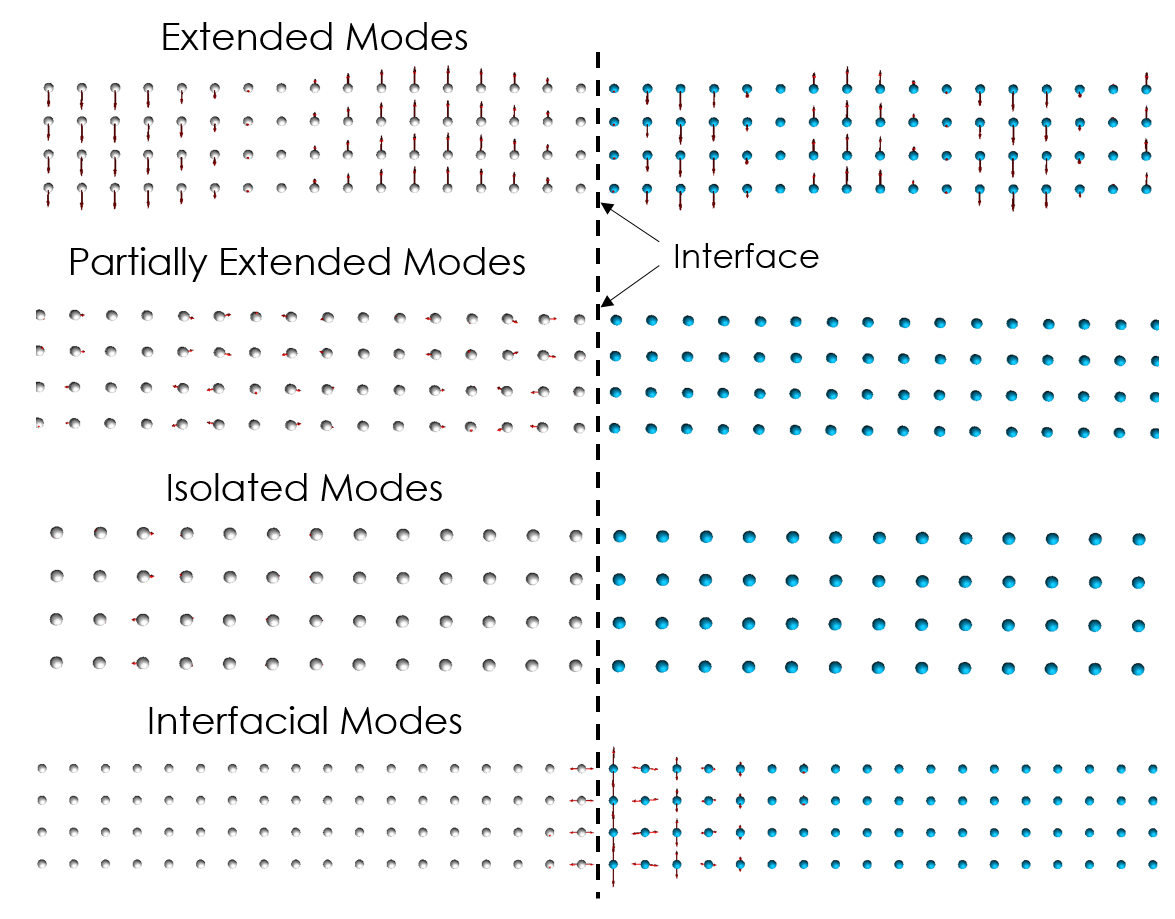
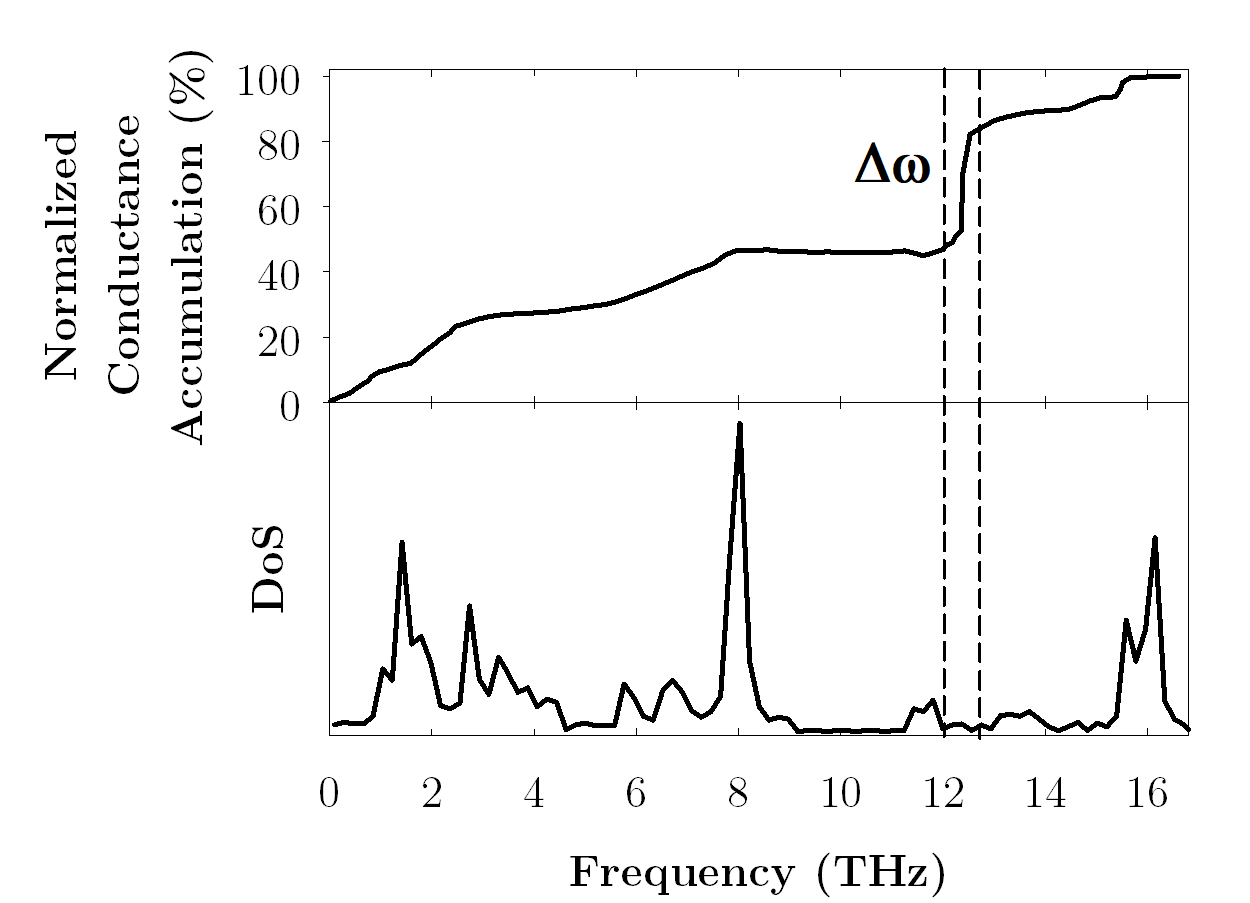
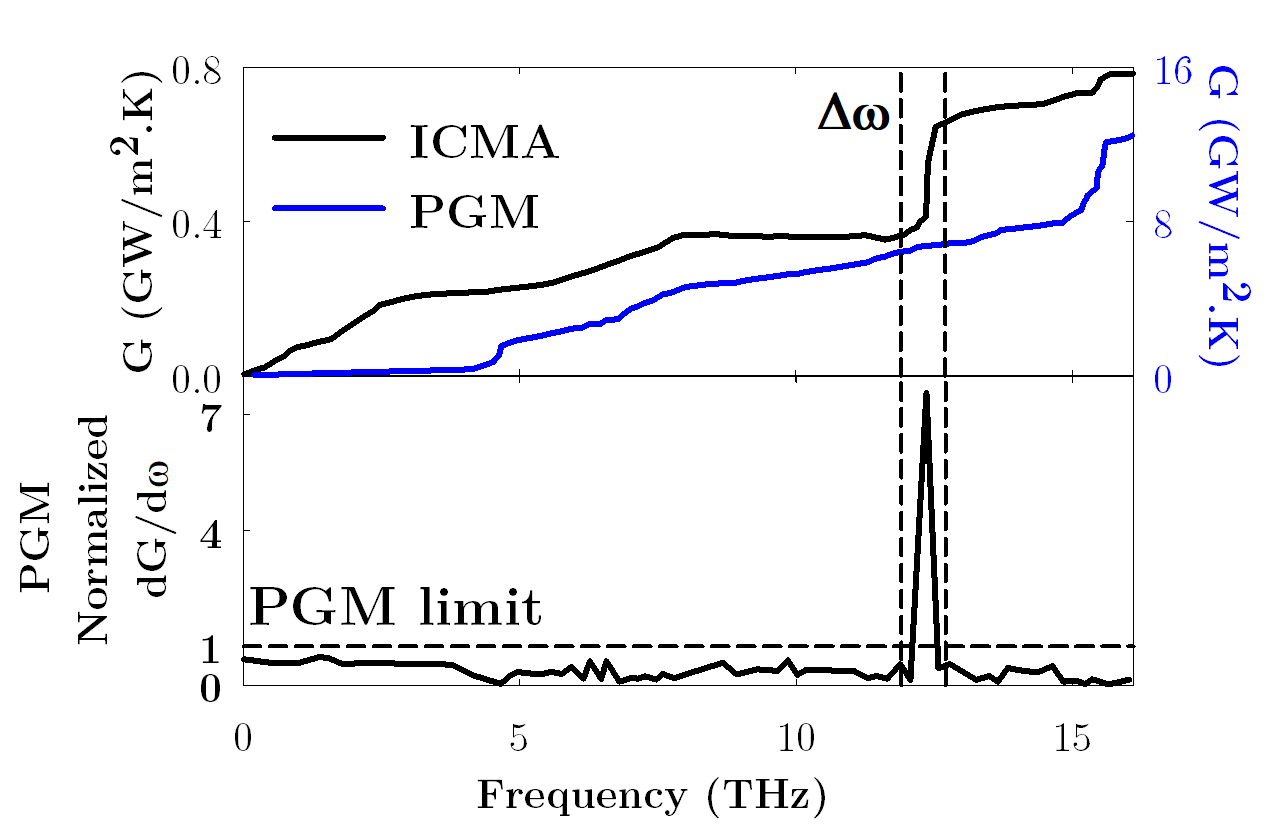
The interface conductance modal analysis (ICMA) method is a formalism we developed to enable the study of phonon transport at interfaces. In essence it is based on the same underlying principle as GKMA, but here it is reformulated for an interface. One of the most interesting things about ICMA is that it treats the problem of phonon transport at an interface in terms of correlation rather than scattering. This is distinctly different from the predominant physical picture that has been used for many decades. While developing ICMA we realized that you have to perform a full super cell lattice dynamics calculation of a combined structure containing both materials to find the right normal modes needed to describe what happens at the interface. What was surprising though, was that different types of modes exist, namely extended modes, partially extended modes, interfacial modes and isolated modes. These new classifications have prompted a rethinking of the more widely accepted physical picture, as our papers have shown a number of non-intuitive behaviors are possible within our new ICMA based paradigm.