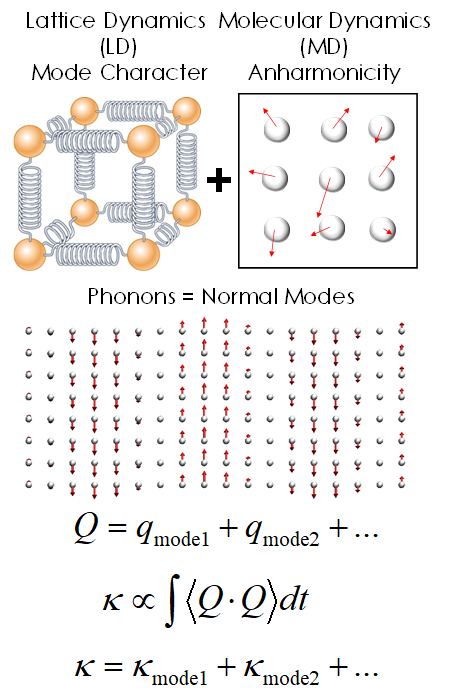
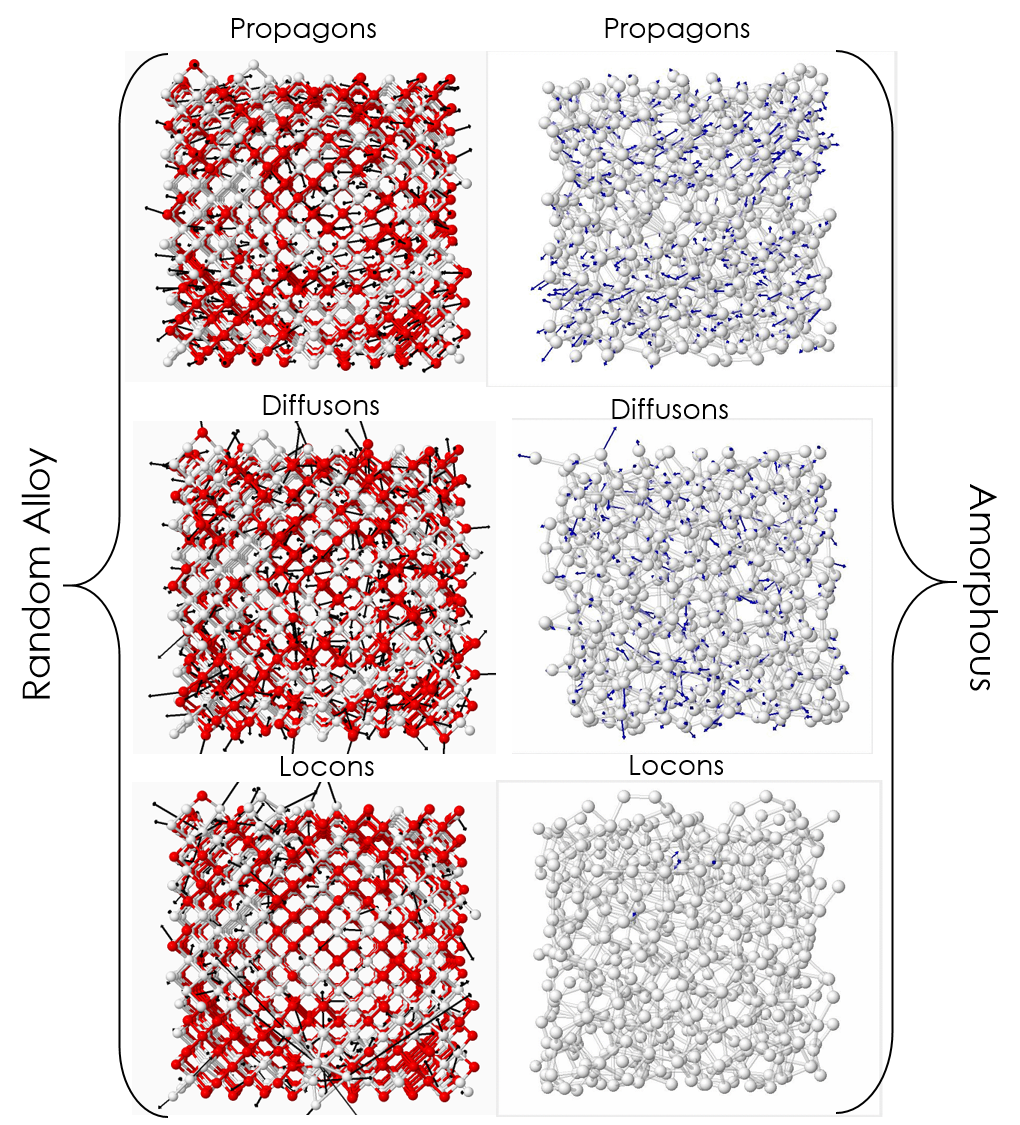
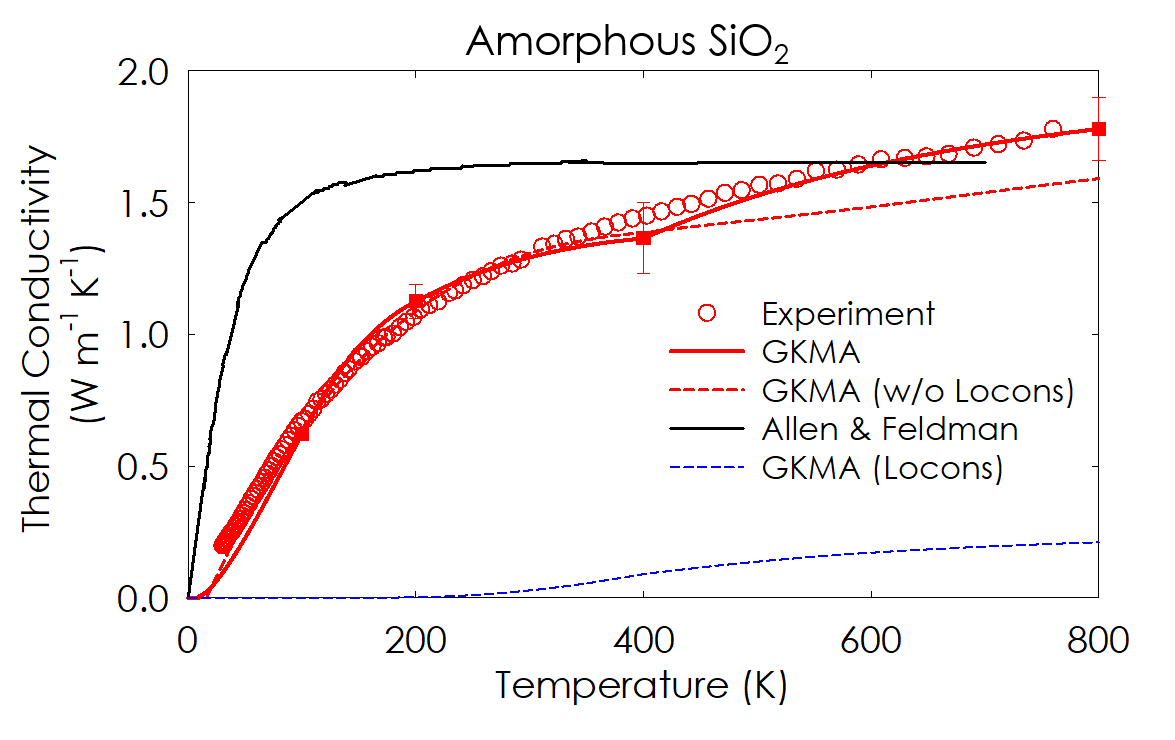
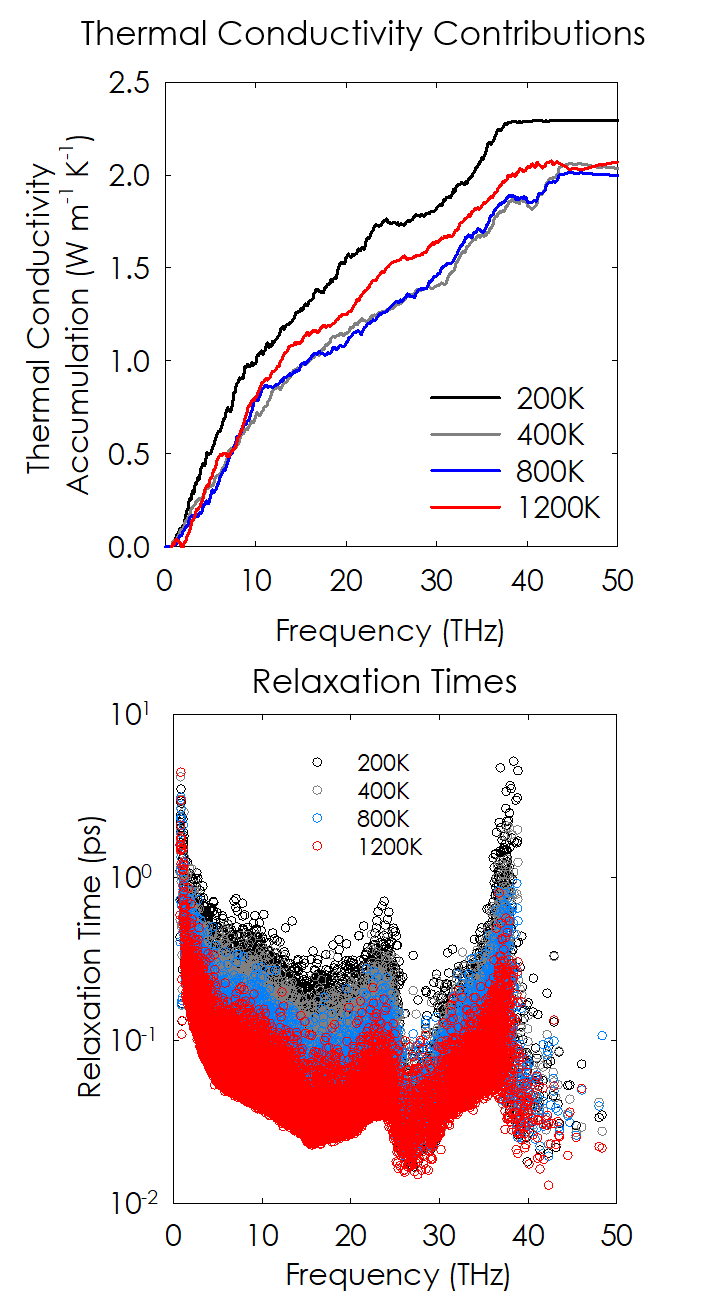
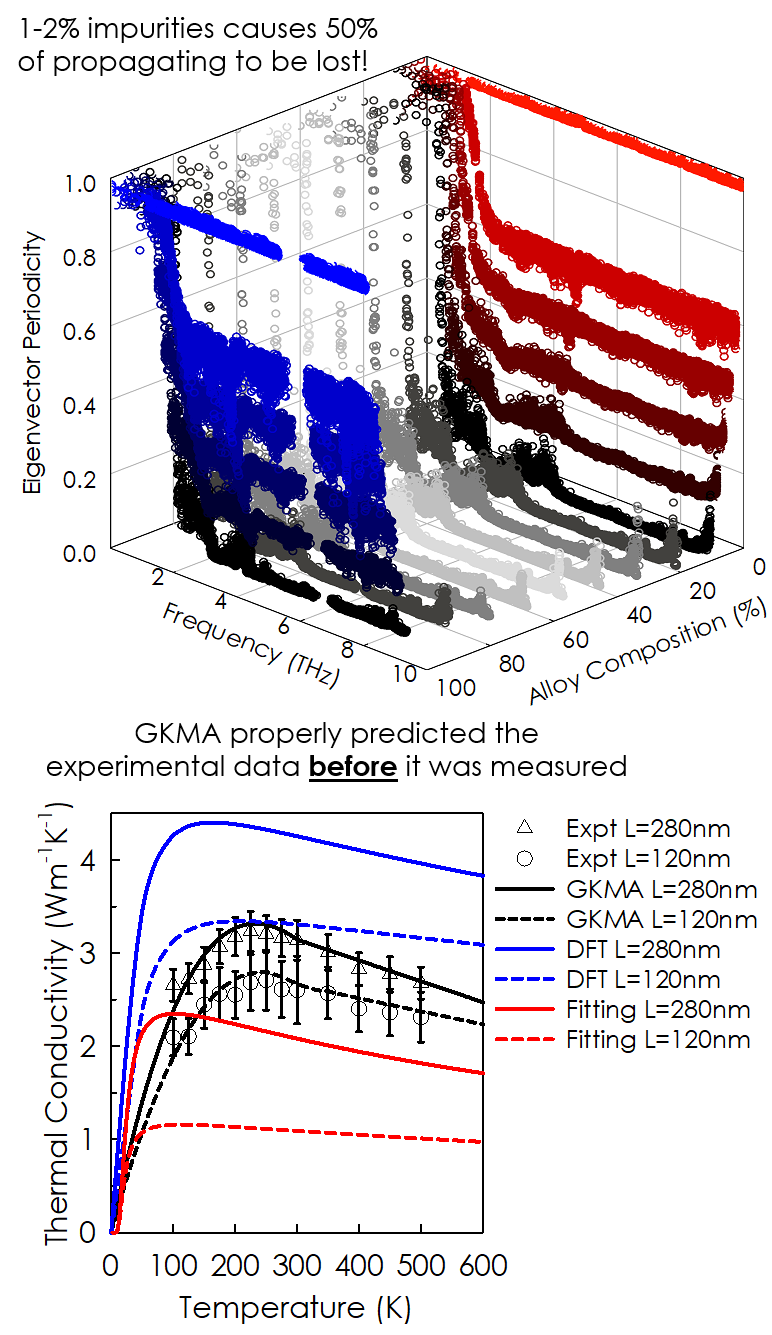
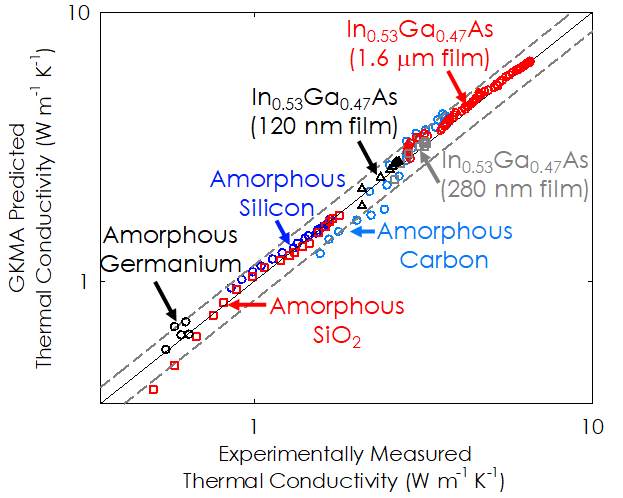
Green-Kubo Modal Analysis (GKMA)

The Green-Kubo Modal Analysis (GKMA) method involves a modal decomposition of the volume averaged heat flux. It merges the lattice dynamics (LD) formalism with molecular dynamics (MD). LD is a framework where one approximates the interactions between atoms as harmonic (i.e., described by linear springs described by Hooke’s law). In this limit, one can solve the equations of motion analytically, and will obtain the normal modes of vibration. The normal modes are the individual solutions to the equations of motion that each have a specific frequency (the eigenvalue) associated with the collective motion (the eigenvector) of the atoms. The modes then serve as a basis set upon which the motion of the atoms can be projected to track the time dependent amplitude for each mode, which reveals information about how the modes are interacting. In reality, the motion of the atoms is not harmonic. It is anharmonic, meaning that there are non-linear aspects to the interactions. Even it is predominantly harmonic, the smaller anharmonic contributions are critical to include, because they are what give rise to thermal resistance – i.e., without anharmonicity the thermal conductivity would become infinite. MD is a simulation procedure where atoms are treated classically as point particles and their motion is described by Newton’s law. A non-linear model for the interactions between atoms, termed the interatomic potential, which is designed to specifically describe the material of interest, is then used to determine the forces on the atoms at a given instant in time. The MD simulation then contains the real anharmonic motion of the atoms and reveals information about the thermal conductivity, via the Green-Kubo formalism. GKMA, however, uses a projection of the heat flux onto the normal modes obtained from LD to then determine the individual contributions to the thermal conductivity.

GKMA reproduces known results for crystals, but where it becomes most powerful is in situations where there is some form of disorder or broken symmetry. When symmetry is broken and all atoms in a material are no longer indistinguishable, the solutions to the equations of motion (i.e., the normal modes) no longer become plane waves as they would in a pure crystalline material. Instead, they take on three classifications, namely propagons, diffusons and locons. Propagons resemble the character of phonon/modes in a crystal, since they look like plane waves and exhibit periodic displacement profiles for the atoms. The diffusons, however, often comprise the majority of the modes and they appear to correspond to random vibrations. The locons are localized, and these three classifications of modes exist in both compositionally disordered (i.e., alloys) and structurally disordered (i.e., amorphous) materials.

When applying GKMA to different materials we consistently observe good agreement with the experimental data. However, one of the advantages of GKMA or other methods is that we can determine how much each class of modes contributes to thermal conductivity. For example, it had previously been believed that locons (the localized modes) could not possibly contribute to thermal conductivity because they are localized (i.e., stuck in one place) and thus cannot participate in moving heat to another location. However, when studying silicon dioxide (i.e., glass) we learned that the locons are responsible for about 10% of the thermal conductivity at high temperature, when their heat capacity becomes substantial. This is one example of a non-intuitive result revealed by GKMA, that suggests a new physical picture for phonons is needed.

Another example of why we’ve come to think that a new physical picture is needed came from studies of both amorphous silicon and silicon dioxide. According to the PGM, the majority of the temperature dependence in thermal conductivity comes from changes in the phonon scattering rates, which is the inverse of the relaxation time. The figure (top) shows that as silicon dioxide gets hotter, the thermal conductivity contributions don’t change much, and the GKMA prediction match experiments. However, the relaxation times change by an order of magnitude over the same temperature range as shown in the figure (bottom). This suggests that the phonon contributions cannot be described by the usual expression associated with the PGM, and therefore further suggests a revised/new physical picture is needed.

Another interesting and non-intuitive result of apply GKMA was the recognition that the shape/character of normal modes changes very quickly as one introduces disorder. The figure (top) shows how closely the modes resemble a periodic plane wave (vertical axis), as a function of the mode frequency and alloy composition (two axes in the horizontal plane) in indium gallium arsenide. Also interesting was the fact that GKMA was able to properly predict the thermal conductivity of the alloy thin films, as shown in the figure (bottom), while both ab initio and a fitting based approach were unable to properly describe what happens. This further points to the fact that the issue with previous theories truly is the physical picture itself, as there’s no set of input parameters that can be rationalized and simultaneously explain the experimental data.

For all the different materials we’ve studied thus far, GKMA has exhibited excellent agreement with experiments across a broad range of temperatures. This points to the utility of using such a general model, which to our knowledge, is the only model currently capable of describing all classes of solids and molecules with a single framework. As we work towards more validation, we are also developing more understanding and generating new ideas for what the more generally applicable physical picture should be for phonons.