Phonon Optimized Potentials

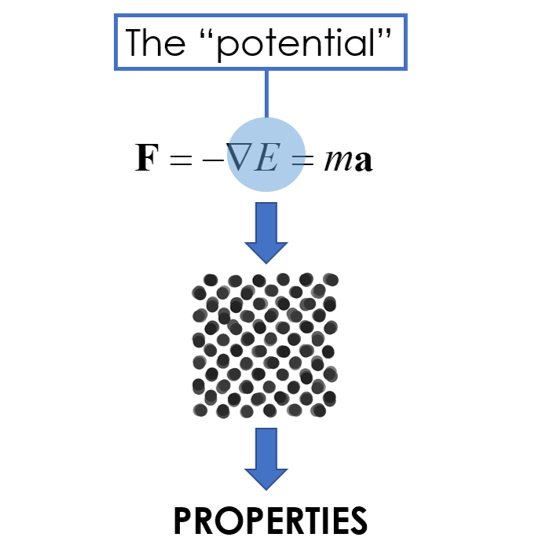
Overview of Potentials

The motion of atoms dictates many material properties, especially thermal properties and heat transfer. We study this motion theoretically by applying Newton’s 2nd law to each atom, where atomic forces arise from the spatial gradient of the potential energy. There are a plethora of methods, some developed by us, to extract bulk material properties from this atomic motion, thus aiding in the low-level understanding and design of material properties.

From the beginning, however, this process requires an accurate representation of interatomic potential energy, which is often represented as an analytical function called the “potential”. Our work involves the design and parameterization of these potentials to calculate accurate molecular dynamics, and therefore study material properties at the molecular level.

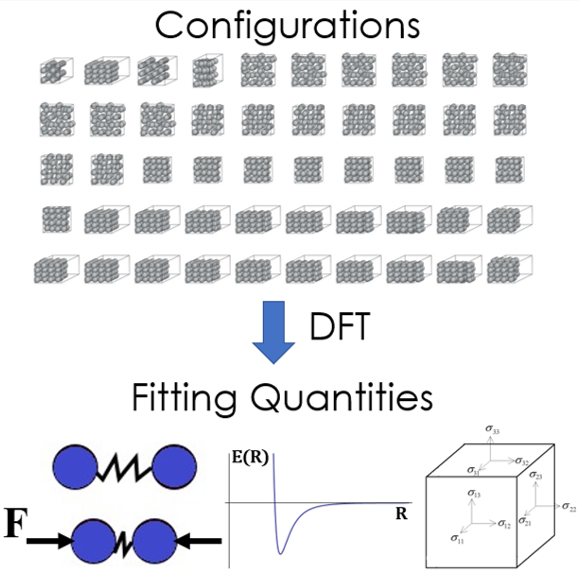
Training Potentials

The process of making potentials starts by generating training data, traditionally consisting of empirically measured quantities. We use quantum mechanical methods such as density functional theory (DFT) which are accurate, but not computationally feasible for simulating length and time scales of engineering interest, to calculate fitting quantities such as forces, energies, and stresses for many configurations of atoms.

To teach the potential to associate quantum mechanical quantities with atomic positions, we minimize the error between quantum mechanical quantities and quantities calculated by the potential, by optimizing the parameters of the potential.

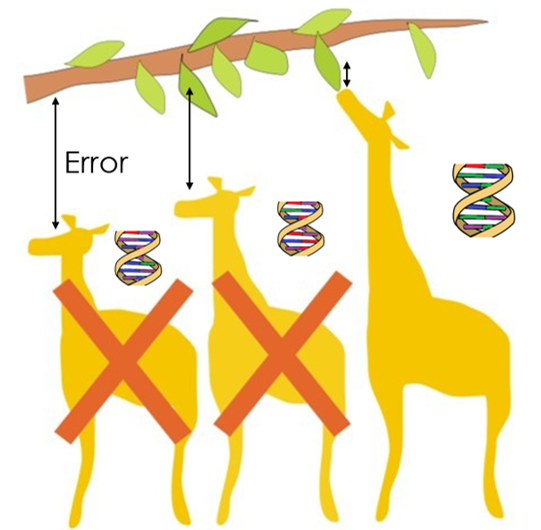
Multidimensional Optimization and Machine Learning

Since potentials can contain dozens of fitting parameters in a large nonlinear search space, we develop computationally efficient multidimensional optimization techniques. The genetic algorithm, for example, mimics natural selection, where populations of individuals such as these giraffes minimize some error, like the distance between their head and the trees, to survive. The fittest individuals pass on their genes, which can be thought of as fitting parameters that get optimized throughout generations.

We perform similar processes to optimize interatomic potentials, where the error to minimize is now between quantum mechanical quantities (e.g. forces, energies, derivatives of energies, etc.) and potential quantities.

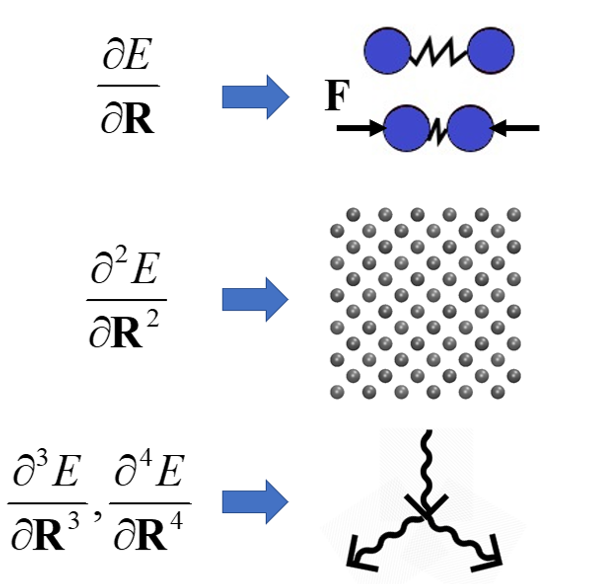
Phonon Optimized Potentails (POPs)

POPs are analytical potentials that accurately reproduce the spatial derivatives of energy. The first derivative is simply the force. The second derivative ensures that we capture accurate harmonic modes of vibration. Third and higher derivatives allow these modes to interact, resulting in thermal conductivity.

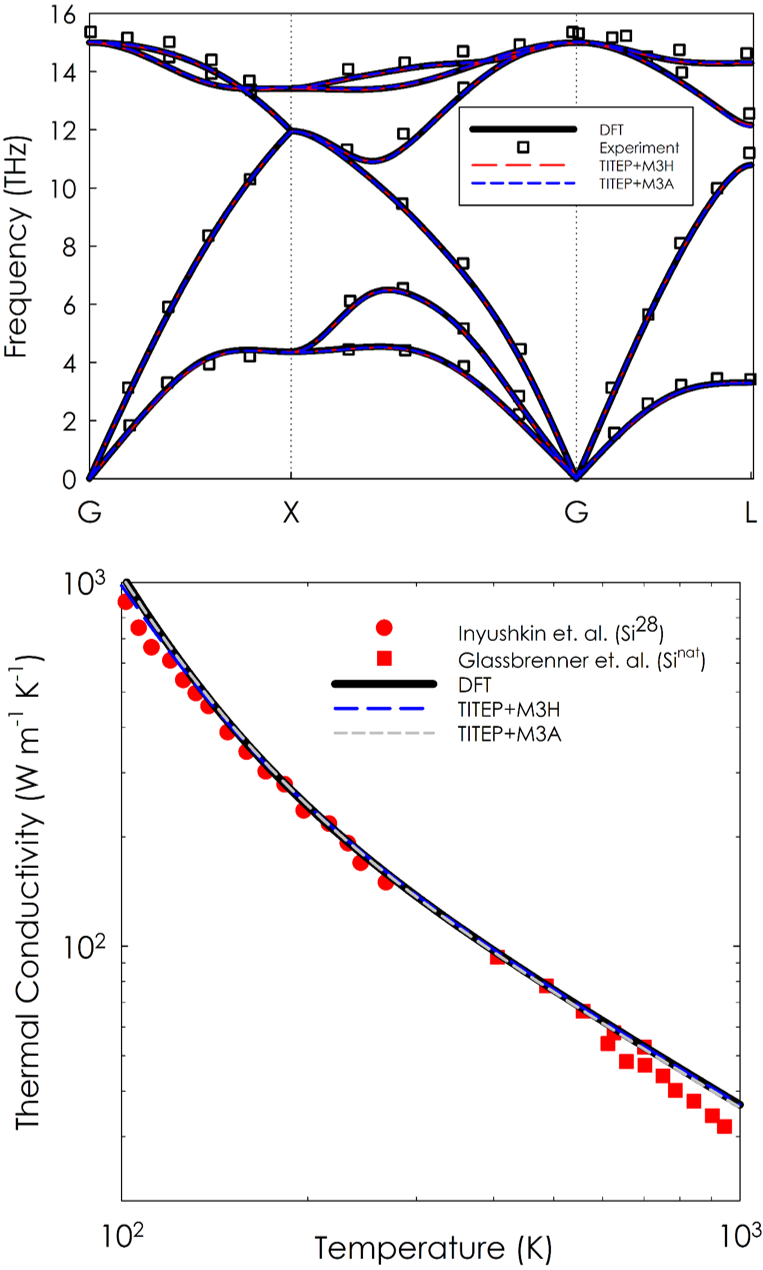
For example, by separating the interatomic potential into two components, i.e., the harmonic (long ranged) and anharmonic (short ranged) portions, we’re able to now fit a Taylor expansion to exactly describe the 2nd derivatives, which ensures correct dispersion and mode shapes, and we use a flexible multi-body functional form for the higher order derivatives, which ensure the mode-mode interactions and therefore thermal conductivity are correct. This advancement serves as a major breakthrough for modeling phonon transport, as it ensures the interactions between atoms are correct and thus the subsequent MD simulations now have the predictive power emboldened by the underlying ab initio calculations used to train the potential.